Transaction Chain
The receiver (Bob) would accept Bitcoins that are sent to his pubic key
The transaction would be signed with the digital signature of the spender (Alice)
The Bitcoins that Alice want to spend was received on one of her public keys
Alice uses her private key to generate the digital signature
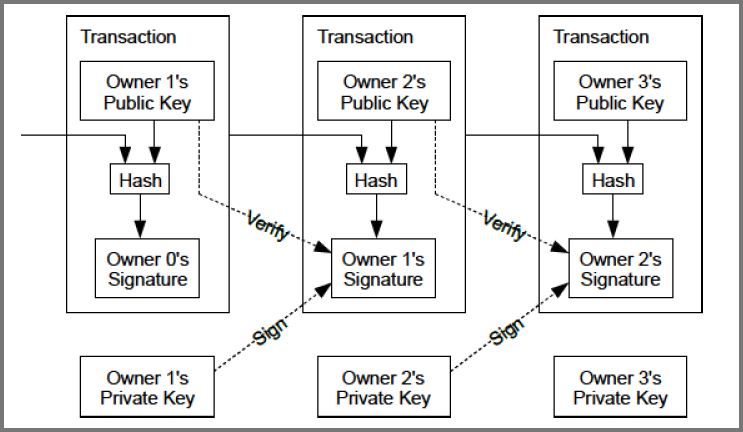
Bob’s public key along with data from the previous transaction are hashed together
This hash is added into the new transactions data field
Alice commits (attests) to this hash using her signature
Since the hash includes Bob’s public key Alice has also committed to it
Full nodes can verify that Alice’s signature committed to the transaction
Public Key Cryptography
Utilizes mathematical functions that are easy to calculate in one direction but infeasible to compute in the opposite direction
Bitcoin uses elliptical curve addition and multiplication as its basis of cryptography
Public Key Cryptography relies on a mathematically linked key pair
In Bitcoin the public key is used to receive funds and the private key is used to sign transactions for spending funds
The mathematical relation between the keys that allows the private key to be used to generate signatures that can be verified using the public key
It is also possible to derive the public key from the private key
Private Key
Bitcoin wallets can have multiple key pairs
The private key is derived from a number that is selected at random
Using elliptical curve multiplication the public key is calculated from the private key
The most important step in key generation is to find source of entropy
Bitcoin uses CSPRNGs to generate 256 bits of entropy
The private key can be a number between 0 and n-1 (inclusive)
n is a very large constant. A 256 bits of entropy that is generated
These bits are sent to a SHA256 hashing function that generates a number
If the number is within the range it can be used as the private key
Elliptical Curve Cryptography (ECC)
It is based on the discrete logarithm problem expressed by addition and multiplication on the points on the elliptical curve
Bitcoin uses a curve called “secp256k1”
Curve Equation:
The modulus p operation is performed so that the value is within a finite range
(Large Prime Number)
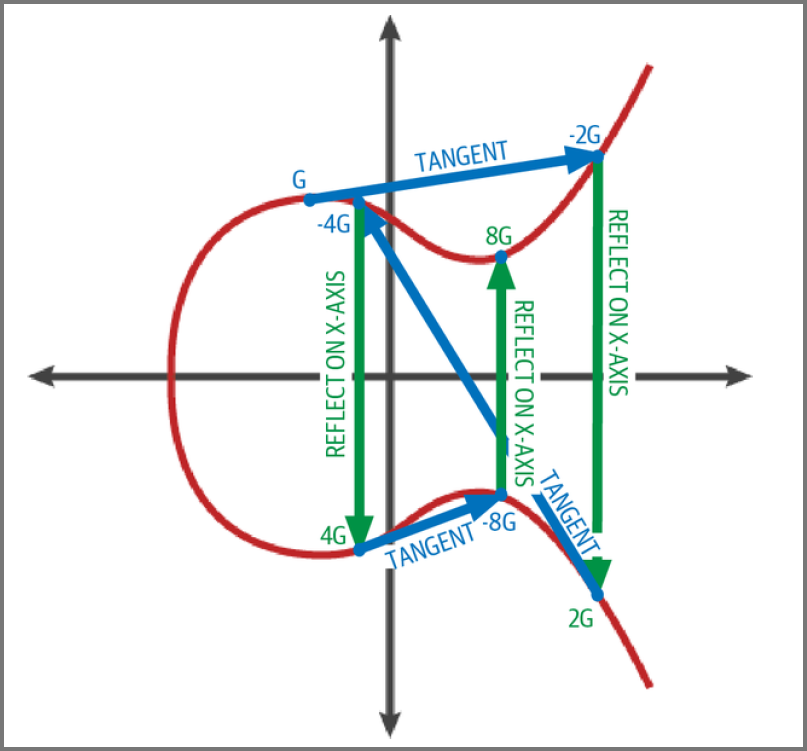
Elliptical curve math has a concept called “Point at Infinity”
This is required for special cases. It is similar to the concept of zero in addition
Represented as x = y = 0
The + operation in elliptical curve math is similar to the addition operator
Given P1 and P2 there is a third point on the curve such that P3 = P1 + P2
Geometrically, P3 is found by drawing a line between P1 and P2 which will interact a additional point. This is P3’ = (x, y) reflect it on the x-axis to get P3 = (x, -y)
If P1 and P2 is the same point and we draw a line between them we will get a tangent that intersects at exactly one additional point
If P1 and P2 have the same x value but different y value the tangent will be vertical
In this situation P3 becomes the Point at Infinity
If P1 is point at infinity then P1 + P2 = P2
If P2 is point at infinity then P1 + P2 = P1
If P is a point on the curve, if k is a whole number then, kP = P + P + P … (k times)
k is sometimes also confusingly referred to as Exponent
Public Key
Public is generated using elliptical curve multiplication
K = Public Key, k = Private Key, G = Generator Point
The reverse operation finding the discrete logarithm is impossible
Functions that are only easy to calculate in one direction is also called “trap door”
G is specified as part of “secp256k1” and is same for all keys in Bitcoin
K (public key) is a point on the elliptical curve (has a x and y co-ordinate)
Computing kG is the same as adding G to itself k times
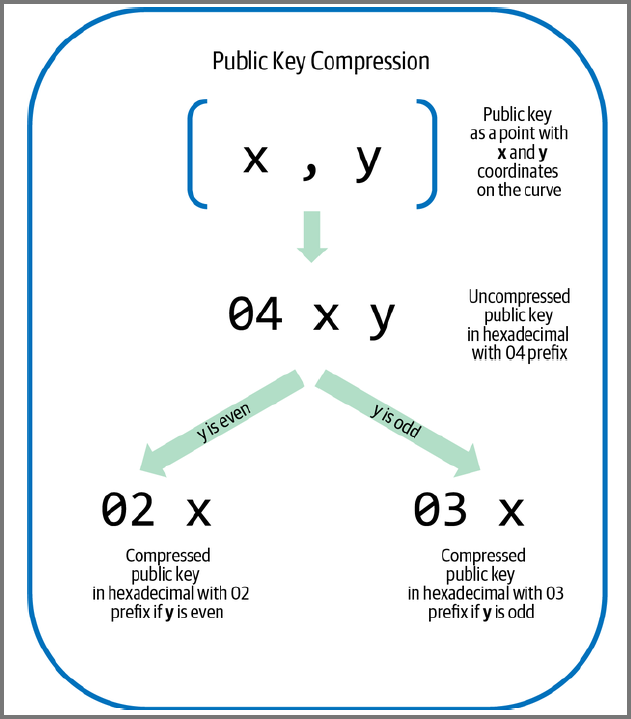
Compressed Public Keys
Initial versions of Bitcoin used a 65-bytes pubic keys
Later a method to save it in 33-bytes was found
This key was backwards compatible so no change was made to Bitcoin protocol
The new key came to be known as “compressed public key”
The original key came to be known as “uncompressed public key”
Smaller keys resulted in smaller transactions because of this more transactions could be included in a block
The public key is a point (x, y) on the elliptical curve
If we know the value of the x we can find the y using the curve equation
By omitting y the space required to store the public key reduces by 256 bits (50%)
Uncompressed keys start with a prefix of 04
Compressed keys start with prefix of 02 or 03
Calculating y using the curve equation will result in two values
The square root of results in a positive and negative point
The points are reflections along the x-axis
While y is not saved we still need to store information about the sign
When y is calculated in binary the resultant value is odd and even (+ve & -ve)
02 means the y coordinate is even and 03 means it is odd
The commitment that is generated from the compressed public key is different from the what is generated from the uncompressed public key even though they have the same private key
New versions of Bitcoin only use compressed public keys
Wallet software need to be able to identify them both as users might have coins in blocks that utilized uncompressed public keys
Bitcoin Addresses
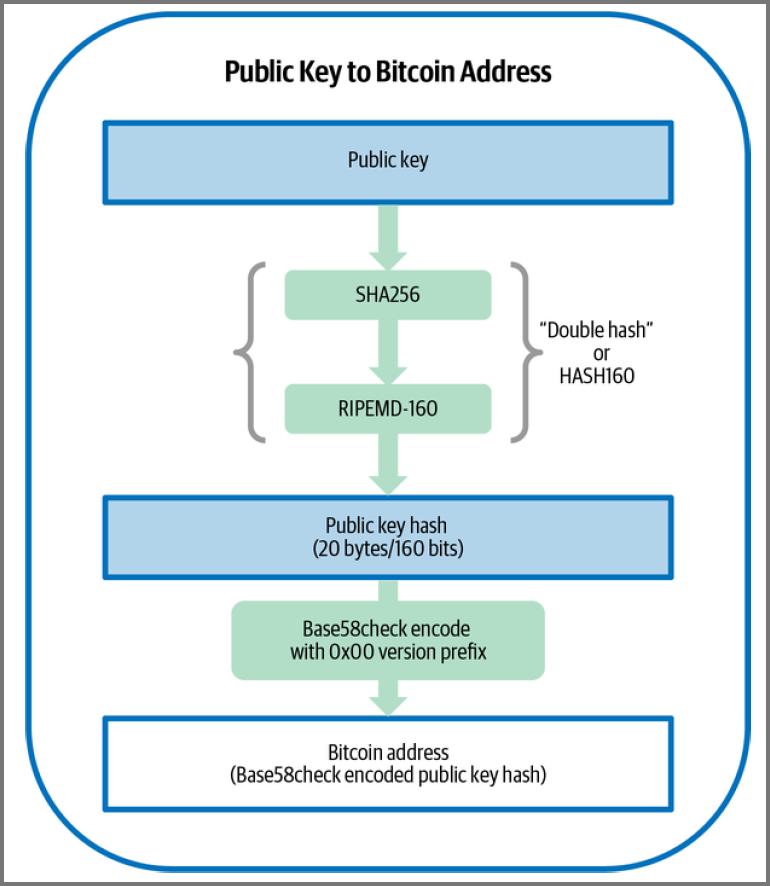
Vanity Addresses
Addresses that contain human readable words
Requires testing billions of private keys to find one the generate a Bitcoin address with the desired pattern
Vanity Pool a service that rewards users with fast systems Bitcoins for finding Vanity addresses